Ø HALF ADDER
Sebuah rangkaian Adder terdiri dari Half Adder dan Full Adder. Half Adder menjumlahkan dua buah bit input, dan menghasilkan nilai jumlahan (sum) dan nilai lebihnya (carry-out). Half Adder diletakkan sebagai penjumlah dari bit-bit terendah (Least Significant Bit). oleh karena itu dinamakan penjumlah tak lengkap.
- Jika A=0 dan B=0 dijumlahkan, hasilnya S (Sum) = 0.
- Jika A=0 dan B=1 dijumlahkan, hasilnya S (Sum) = 1.
- Jika A=1 dan B=1 dijumlahkan, hasilnya S (Sum) = 0. dengan nilai pindahan Ce(Carry Out) = 1.
Dengan demikian, half adder memiliki 2 masukan (A dan B) dan dua keluaran (S dan Ce)
A
|
B
|
H
|
Ce
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
Dari tabel di atas, perhatikanlah sinyal " 1 " pada “H” dan “Ce” dapat dikembangkan persamaan fungsi seperti di bawah ini.
Hasil .
H = ( A Λ B ) v ( A Λ B ) = A v B ( Ex - OR )
Ce = A Λ B ( AND )
Dari kedua persamaan di atas dapat dikembangkan rangkaian Half Adder seperti di bawah ini.
Ø FULL ADDER
Half Adder tidak dapat digunakan untuk melakukan proses penjumlahan dua buah bilangan yang masing-masing terdiri dari beberapa digit ( multi digit ). Penjumlahan yang terdiri dari beberapa bit harus menyertakan carry pada digit yang lebih tinggi berikutnya dan solusi penjumlah yang demikian disebut Full Adder ( FA ), dimana disamping input A dan B disertakan juga Carry sebagai bagian dari input.
Tabel kebenaran dari Full Adder
A
|
B
|
Ci
|
H
|
Ce
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
= ( A Λ B Λ Ci ) v ( A Λ B Λ Ci ) v ( A Λ B Λ Ci ) v ( A Λ B Λ Ci )
Sesuai Hukum Distributive pada Aljabar Boole, persamaan fungsi di atas menjadi,
H = [ ( A Λ B ) v ( A Λ B ) ] Λ Ci v [ ( A Λ B ) v ( A Λ B ) ] Λ Ci
= [ ( A Λ B ) v ( A Λ B ) ] Λ Ci v ( 1 Λ Ci )
= [ ( A Λ B ) v ( A Λ B ) ] Λ ( Ci v Ci )
= ( A V B ) V C = A V B V C
Disamping persamaan Hasil juga terdapat persamaan untuk Carry seperti di bawah ini,
Ce = ( A Λ B Λ Ci ) v ( A Λ B Λ Ci ) v ( A Λ B Λ Ci ) v ( A Λ B Λ Ci )
Persamaan ini dapat disederhanakan menjadi,
Ce = ( A Λ B ) v ( B Λ Ci ) v ( A Λ Ci )
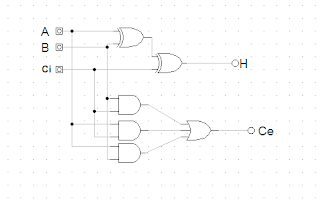
Dari kedua persamaan di atas dapat dikembangkan menjadi rangkaian digital Full Adder .
kebenaran dari Full Adder :








0 Komentar:
Post a Comment