Mengenal K-Map ( Karnaugh Map )

K-Map ( Karnaugh Map )

Karnaugh Map atau yang biasanya disebut dengan K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan. K-Map terdiri dari kotak-kotak yang jumlahnya terdiri dari jumlah variable dan fungsi logika atau jumlah inputan dari rangkaian logika yang sedang kita hitung.

            Rumus untuk menentukan jumlah kotak pada K-Map adalah 2ⁿ n adalah banyaknya variabel / inputan.

Langkah – langkah pemetaan K-Map secara umum :

·        Menyusun aljabar Boolean terlebih dahulu

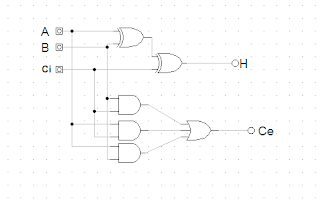
·        Menggambar rangkaian digital

·        Membuat Table Kebenarannya

·        Merumuskan Tabel Kebenarannya

·        Lalu memasukkan rumus Tabel Kebenaran ke K-Map (Kotak-kotak

Penyederhanaan Dua Variabel

Catatan : Bar = ‘

Tabel dari K-Map 2 variabel adalah seperti dibawah ini

Contoh Soal
H = AB + A’B+AB’

Maka cara pengerjaanya seperti dibawah ini

Bar / ‘ biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar / ‘

Dan dapat dipermudah lagi menjadi dibawah ini

Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya

Yaitu terletak pada kotak 01 + 11 dan 10 + 11 yaitu cara penyederhanaan dengan cara menulis angka yang sama (1 lingkaran) dan menerjemahkannya kedalam bentuk huruf seperti A dan B.

Caranya :

01

11

  1        yang sama adalah angka 1 yang dibelakang jadi jika letaknya dibelakang (kedua) adalah B (B diambil dari tabel K-Map Diatas ) jika yang sama angka 0 pada urutan kedua adalah B’ diatas sudah disebutkan bahwa angka 0 = Bar/’

10

11

1          yang sama adalah angka 1 yang didepan jadi jika letaknya didepan (pertama) adalah A (A diambil dari tabel K-Map Diatas) jika yang sama angka 0 pada urutan kedua adalah A’ diatas sudah disebutkan bahwa angka 0 = Bar/’

Jadi kesimpulan dari contoh diatas adalah dari rumus :

H = AB + A’B + AB’ dapat disederhanakan menggunakan K-Map menjadi

BA / AB (boleh dibalik menurut abjad tetapi harus 1 teman atau tidak dapat dibalik dengan huruf yang dipisahkan dengan penjumlahan atau pengurangan)

Penyederhanaan Tiga Variabel

Catatan : Bar = ‘

Tabel dari K-Map 3 variabel adalah seperti dibawah ini

Contoh Soal
H = ABC + A’BC+A’B’C+AB’C

Maka cara pengerjaanya seperti dibawah ini

Bar / ‘ biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar / ‘

Dan dapat dipermudah lagi menjadi dibawah ini

Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya

Cara diatas adalah langsung mesederhanakan 4 kotak, sebenarnya dapat disederhanakan menjadi 2 kotak 2 kotak tetapi terlalu lama dan kita hanya menyingkat waktu saja menjadi 4 kotak langsung, terletak pada kotak 001 + 011+101 +111 yaitu cara penyederhanaan dengan cara menulis angka yang sama (1 lingkaran) dan menerjemahkannya kedalam bentuk huruf seperti A, B, C.

Caranya :

011

011

101

111

     1     yang sama adalah angka 1 yang dibelakang jadi jika letaknya dibelakang (keempat) adalah C (C diambil dari tabel K-Map Diatas ). Jika yang sama angka 0 pada urutan keempat adalah C’ diatas sudah disebutkan bahwa angka 0 = Bar/’

Jadi kesimpulan dari contoh diatas adalah dari rumus :

H = ABC + A’BC+A’B’C+AB’C dapat disederhanakan menggunakan K-Map menjadi C.

Penyederhanaan 4 variabel

Catatan : Bar = ‘

Tabel dari K-Map 4 variabel adalah seperti dibawah ini

Contoh Soal
H = ABCD + ABCD’+AB’CD+ABC’D’

Maka cara pengerjaanya seperti dibawah ini

Bar / ‘ biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar / ‘

Dan dapat dipermudah lagi menjadi dibawah ini

Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya

Yaitu terletak pada kotak 1111 + 1011 dan 1111 + 1110 dan 1110 + 1100. Cara diatas menyederhanakannya dapat dari sisi paling kanan dengan sisi paling kiri dalam 1 baris.

Cara penyederhanaan dengan cara menulis angka yang sama (1 lingkaran) dan menerjemahkannya kedalam bentuk huruf seperti A, B, C, D.

Caranya :

1111

1011

1  11   yang sama adalah angka 1 yang pertama, ketiga, dan keempat adalah A, C, dan D (A, C, dan D diambil dari tabel K-Map Diatas ) jika yang sama angka 0 pada urutan kedua adalah A’ dst diatas sudah disebutkan bahwa angka 0 = Bar/’

1111

1110

111     yang sama adalah angka 1 yang pertama, kedua, dan ketiga adalah A, B, C (A, B, C diambil dari tabel K-Map Diatas) jika yang sama angka 0 pada urutan kedua adalah A’ dst diatas sudah disebutkan bahwa angka 0 = Bar/’

1110

1100

11       yang sama adalah angka 1 yang pertama dan kedua adalah A dan B (A dan B diambil dari tabel K-Map Diatas) jika yang sama angka 0 pada urutan kedua adalah A’ dst diatas sudah disebutkan bahwa angka 0 = Bar/’

Jadi kesimpulan dari contoh diatas adalah dari rumus :

H = AB + A’B + AB’ dapat disederhanakan menggunakan K-Map menjadi

ACD + ABC + AB (boleh dibalik menurut abjad tetapi harus 1 teman atau tidak dapat dibalik dengan huruf yang dipisahkan dengan penjumlahan atau pengurangan)

Read More

Mengenal Multiplexer & Demultiplexer

Multiplexer & Demultiplexer

Multiplexer (Mux) adalah suatu komponen elektronika yang fungsinya adalah sebagai penyeleksi data berdasarkan perintah untuk menampilkan data yang diinginkan. Jadi singkatnya multiplexer memiliki banyak input data (4,8,dst) tetapi hanya memiliki sebuah output dan memiliki bagian input pengontrol. Jadi, melalui bagian input pengontrol inilah kita dapat menampilkan data input yang dikehendaki.

Salah satu contoh IC mux yang sering digunakan adalah IC 74LS151. IC tersebut merupakan IC multiplexer 8 to 1. Artinya adalah IC tersebut memilik1 8 input data dengan 1 output. Nah, karena input datanya ada 8, maka input pengontrolnya otomatis ada 3 (3bit), alasannya karena jangkauan nilai dari 3 bit data adalah 0 (000) hingga 7 (111).

Gambar 3 : Tabel Kebenaran IC 74LS151 (strobe = output enable, H = 1, L = 0)

Dari tabel diatas tentu kita sudah dapat memahami bagaimana cara kerja dari sebuah IC multiplexer. Contohnya adalah apabila kita ingin menampilkan data pada input D6 (ditampilkan pada output Y), maka pada strobe / OE harus diberi logika 0 dan pada input pengontrol (C,B,A) diberi nilai logika 110 (C=1, B=1, A=0). Nilai output W adalah negasi dari output Y. Hasil simulasi IC 74LS151 menggunakan proteus.

  

Gambar diatas adalah contoh sederhana dari prinsip kerja sebuah multiplexer. Ketika pada input (CBA) diberi nilai 010, maka pada output Y akan menampilkan data yang masuk pada input X2 (D2). Dan pada output Y (W) akan menampilkan negasi dari output Y. 
Untuk membuktikan bahwa data yang ditampilkan pada output Y adalah data yang masuk pada input X2 (D2), nilai data pada X2 (D2) diubah. Dan setelah nilai X2 diubah, maka nilai output Y juga akan berubah sesuai dengan nilai X2.

   

Demultiplexer adalah rangkaian logika yang menerima satu input data digital dan mendistribusikan input tersebut ke beberapa output.
Demultiplexer mengambil beberapa input dan menyalurkan salah satu dari input tersebut ke output. Demultiplexer melakukan operasi yang sebaliknya. Yaitu mengambil satu input tunggal dan mendistribusikannya ke beberapa output. Dengan kata lain, demultiplexer mengambil satu sumber data input dan secara selectif mendistribusikannya ke salah satu dari N chanel – chanel output. Gambar dibawah ini menunjukkan diagram umum demultiplexer.  

Diagram Umum Demultiplexer 

Gambar Demultiplexer 1 ke 4

Tabel Kebenaran Demultiplexer 1 ke 4

Read More

Mengenal Half Adder Dan Full Adder

Ø  HALF ADDER 

Sebuah rangkaian Adder terdiri dari Half Adder dan Full Adder. Half Adder menjumlahkan dua buah bit input, dan menghasilkan nilai jumlahan (sum) dan nilai lebihnya (carry-out). Half Adder diletakkan sebagai penjumlah dari bit-bit terendah (Least Significant Bit). oleh karena itu dinamakan penjumlah tak lengkap.

1. Jika A=0 dan B=0 dijumlahkan, hasilnya S (Sum) = 0.
2.  Jika A=0 dan B=1 dijumlahkan, hasilnya S (Sum) = 1.
3. Jika A=1 dan B=1 dijumlahkan, hasilnya S (Sum) = 0. dengan nilai pindahan Ce(Carry Out) = 1.

Dengan demikian, half adder memiliki 2 masukan (A dan B) dan dua keluaran (S dan Ce)

A	B	H	Ce
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Dari tabel di atas, perhatikanlah sinyal " 1 "  pada “H” dan “Ce” dapat dikembangkan persamaan fungsi seperti di bawah ini.

Hasil .

H = ( A Λ B ) v ( A Λ B ) = A v B       ( Ex - OR )

Ce = A Λ B                                          ( AND )

Dari kedua persamaan di atas dapat dikembangkan rangkaian Half Adder seperti di bawah ini.

Ø  FULL ADDER

Half Adder tidak dapat digunakan untuk melakukan proses penjumlahan dua buah bilangan yang masing-masing terdiri dari beberapa digit ( multi digit ). Penjumlahan yang terdiri dari beberapa bit harus menyertakan carry pada digit yang lebih tinggi berikutnya dan solusi penjumlah yang demikian disebut Full Adder ( FA ), dimana disamping input A dan B disertakan juga Carry sebagai bagian dari input.

Tabel kebenaran dari Full Adder

A	B	Ci	H	Ce
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

= ( A Λ B Λ Ci ) v ( A Λ B Λ Ci ) v ( A Λ B Λ Ci ) v ( A Λ B Λ Ci )

Sesuai Hukum Distributive pada Aljabar Boole, persamaan fungsi di atas menjadi,

H         = [ ( A Λ B ) v ( A Λ B ) ] Λ Ci v [ ( A Λ B ) v ( A Λ B ) ] Λ Ci

= [ ( A Λ B ) v ( A Λ B ) ] Λ Ci v ( 1 Λ Ci )

= [ ( A Λ B ) v ( A Λ B ) ] Λ ( Ci v Ci )

 = ( A V B ) V C = A V B V C

Disamping persamaan Hasil juga terdapat persamaan untuk Carry seperti di bawah ini,

Ce = ( A Λ B Λ Ci ) v ( A Λ B Λ Ci ) v ( A Λ B Λ Ci ) v ( A Λ B Λ Ci )

Persamaan ini dapat disederhanakan menjadi,

Ce = ( A Λ B ) v ( B Λ Ci ) v ( A Λ Ci )

Dari kedua persamaan di atas dapat dikembangkan menjadi rangkaian digital Full Adder .

kebenaran dari Full Adder :

Read More